Задача
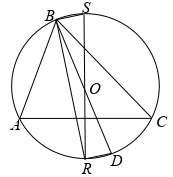
Из центра $O$ описанной окружности Ω треугольника $ABC$ опустили перпендикуляры $OP$ и $OQ$ на биссектрисы внутреннего и внешнего углов при вершине $B$.
Докажите, что прямая $PQ$ делит пополам отрезок, соединяющий середины сторон $CB$ и $AB$.
Решение
Проведём гомотетию с центром $B$ и коэффициентом 2. Точка $O$ перейдёт в точку $D$, диаметрально противоположную вершине $B$, точка $P$ – в точку $R$ пересечения биссектрисы угла $B$ с Ω, точка $Q$ – в диаметрально противоположную $R$ точку $S$, "отрезок, соединяющий..." – в сторону $AC$. Осталось заметить, что диаметр $RS$ проходит через середину стороны $AC$, так как $R$ – середина дуги $AC$.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет