Задача
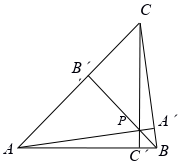
Отрезки $AA', BB'$ и $CC'$ с концами на сторонах остроугольного треугольника $ABC$ пересекаются в точке $P$ внутри треугольника. На каждом из этих отрезков как на диаметре построена окружность, в которой перпендикулярно этому диаметру проведена хорда через точку $P$. Оказалось, что три проведённые хорды имеют одинаковую длину. Докажите, что $P$ – точка пересечения высот треугольника $ABC$.
Решение
Пусть 2$x$ – длина указанных хорд. По теореме о произведении отрезков хорд $x^{2} = AP\cdot A'P = BP\cdot B'P = CP\cdot C'P$. По обратной теореме точки $A, A', B$ и $B'$ лежат на одной окружности. Значит,
∠$AA'B$ = ∠$AB'B$. Аналогично ∠$AA'C$ = ∠$AC'C$, ∠$BB'C$ = ∠$BC'C$. Следовательно, ∠$AA'B$ = ∠$AB'B$ = 180° – ∠$BB'C$ = 180° – ∠$BC'C$ = ∠$AC'C$ = ∠$AA'C$, то есть $AA'$ – высота. Аналогично $BB'$ и $CC'$ – высоты.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь