Решение 1:   Если Петя возьмёт себе все черви, все тузы, короли и дамы, то Вася не сможет набрать очки на тузе, короле и даме червей, т.е. наберёт не больше 15 очков.

  Переформулируем задачу. Рассмотрим доску 4×9. Петя закрашивает чёрным 18 клеток. Докажем, что Вася сможет выделить не менее 15 непересекающихся хороших пар: в каждой паре две клетки разного цвета, находящиеся в одной строке или одном столбце.

  Назовём весом столбца количество чёрных клеток в нём. Сначала Вася рассматривает столбцы типа 2 (если они есть). Каждый из них, очевидно, разбивается на две хорошие пары.

  Далее Вася рассматривает пары столбцов типа 0 и 4. Каждая такая пара, очевидно, разбивается на четыре хорошие пары клеток.

  Далее Вася рассматривает пары столбцов типа 1 и 3 (см. рисунки). Каждая такая пара тоже разбивается на четыре хорошие пары клеток (см. рисунки).

  Когда указанные пары столбцов закончатся, в силу симметрии можно считать, что "необработанными" останутся только столбцы типов 4 и 1. Если это $a$ столбцов типа 4 и $b$ столбцов типа 1, то  $4a + b = 3b$,  то есть  $b = 2a$.  В тройке из столбца типа 4 и двух столбцов типа 1 Вася сможет выделить не менее пяти хороших пар клеток (см. рисунки).

  Так как  $3a = a + b \leqslant 9$,  то на всей доске останется не более трёх нехороших пар, т.е. Вася "потеряет" не больше 3 очков.

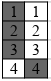
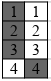
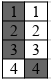
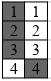
Решение 2:   Воспользуемся известной леммой Холла о сватовстве (см. решение задачи 198160).

  В терминах решения 1 объявим чёрные клетки юношами, белые – девушками, а знакомыми – клетки, находящиеся в одном ряду. Докажем, что для каждой группы из $k$ юношей  ($k$ = 1, 2, ..., 18) имеется по крайней мере  $k - 3$  девушки, имеющих знакомых среди этой группы юношей. Добавив трёх виртуальных девушек, знакомых со всеми юношами, мы окажемся в условиях леммы Холла. Переженив всех юношей и отбросив не более чем троих, которым достались виртуальные девушки, получим не менее 15 хороших пар.

  Пусть есть группа $X$ из $k$ юношей (чёрных клеток). Переставим столбцы, их содержащие, влево, а строки – вниз. Пересечение этих строк и столбцов – прямоугольник площади $S_{1}$ – содержит $X$,

а дополнение к их объединению – прямоугольник площади $S_{2}$ – содержит всех незнакомых с ними девушек. Значит,  $k \leqslant \min(S_{1}, 18)$,  а количество знакомых с ними девушек не меньше  $18 - \min (S_{2}, 18)$.  Достаточно доказать, что  $18 - \min(S_{2}, 18) \geqslant \min(S_{1}, 18) - 3$,  т.е. что  $\min(S_{1}, 18) + \min(S_{2}, 18)$ ≤ 21.

  Выражение  $F = \min(S_{1}, 18) + \min(S_{2}, 18)$  симметрично, поэтому достаточно рассмотреть случай, когда общая вершина $A$ построенных прямоугольников лежит в верхней половине доски. Тогда  $S_{2} \leqslant 18$. 

  Отбросим очевидный случай, когда $A$ лежит на границе доски (тогда  $S_{1}$ = 0  или  $S_{2}$ = 0).  Если  $S_{1}$ < 18,  можно сдвинуть $A$ вправо, чтобы стало  $S_{1}$ = 18  (поскольку 18 делится как на 2,

так и на 3), при этом  $F = S_{1} + S_{2}$  не уменьшится. Если  $S_{1}$ > 18,  можно сдвинуть $A$ влево, чтобы стало  $S_{1}$ = 18,  при этом  $F = 18 + S_{2}$  увеличится.

  Остался единственный случай  $S_{1} = 18,  S_{2} = 3$,  а в нём неравенство выполнено.

15 очков.