Задача
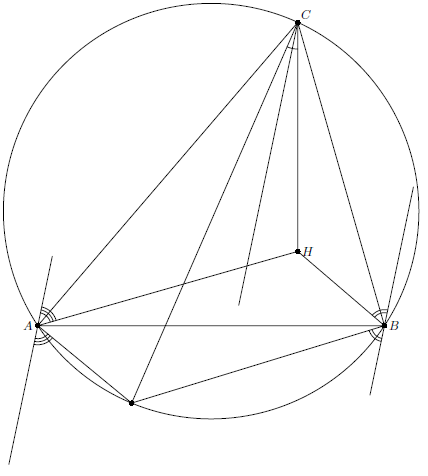
Через вершины треугольника $ABC$ проведены параллельные прямые $l_a$, $l_b$, $l_c$. Пусть прямая $a$ симметрична высоте $AH_a$ относительно $l_a$. Аналогично определяем $b$, $c$. Докажите, что $a$, $b$, $c$ пересекаются в одной точке.
Решение
Поскольку угол между прямыми $a$ и $b$ равен углу между высотами треугольника, точка пересечения этих прямых лежит на окружности, симметричной относительно $AB$ окружности $ABH$ ($H$ – ортоцентр), т.е. на описанной окружности треугольника $ABC$. Прямая $c$ пересекает описанную окружность в той же точке.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет