Задача
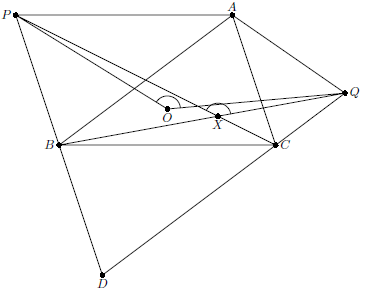
Дан остроугольный треугольник $ABC$. Точка $P$ выбрана так, что $AP=AB$ и $PB \parallel AC$. Точка $Q$ выбрана так, что $AQ=AC$ и $CQ \parallel AB$. Отрезки $CP$ и $BQ$ пересекаются в точке $X$. Докажите, что центр описанной окружности треугольника $ABC$ лежит на окружности $(PXQ)$.
Решение
Пусть $D$ – вершина параллелограмма $ABDC$. Тогда $APDC$ и $AQDB$ – равнобедренные трапеции. Следовательно, серединные перпендикуляры к отрезкам $PD$ и $QD$ совпадают с серединными перпендикулярами к $AC$ и $AB$ соответственно, т.е. центр $O$ описанной окружности треугольника $ABC$ является также центром окружности $DPQ$ и $\angle POQ=2\angle A$. Кроме того, из равенств $\angle XPD=\angle ADP$, $\angle XQD=\angle ADQ$ получаем, что $\angle PXQ=2\angle A$. Таким образом, $O$, $P$, $Q$, $X$ лежат на одной окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь