Олимпиадная задача о четырёхугольниках: вырезание копий
Задача
Верно ли, что из любого выпуклого четырёхугольника можно вырезать три уменьшенные вдвое копии этого четырёхугольника?
Решение
Докажем, что можно выбрать такой угол четырёхугольника, что сумма его с каждым из соседних углов не превосходит развёрнутого угла. Действительно, сумма каких-то двух соседних углов не превосходит 180°. Пусть это углы $A$ и $D$. Тогда, если $\angle A + \angle B$ ≤ 180°, то мы получили нужное, а если $\angle A + \angle B$ > 180°, то $\angle C + \angle D$ < 180°, и нам подходят углы $A, D, C$. В итоге можно так назвать вершины четырёхугольника $A, B, C, D$, что $\angle A + \angle B$ ≤ 180°, $\angle A + \angle D$ ≤ 180°. Пусть $K, L, M, N, P, Q$ – середины отрезков $AB, BC, CD, DA, AC, BD$ соответственно. Четырёхугольники $AKPN, KBLQ, NQMD$ – искомые копии. Докажем, что они не перекрываются. Действительно, $\angle AKP + \angle QKB = \angle A + \angle B$ ≤ 180°, $\angle DNQ + \angle ANP$ ≤ 180°. 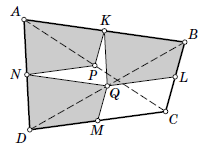
Ответ
Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь