Пусть  $AB$ = 2,  $O$ и $M$ – середины отрезков $AB$ и $YZ$ соответственно, $H$ – ортоцентр треугольника $XYZ$. Поскольку треугольник $XYZ$ равнобедренный, точка $H$ лежит на серединном перпендикуляре к стороне $YZ$, то есть в плоскости π, перпендикулярной $AB$ и проходящей через $O$. Точка $X$ лежит на окружности Ω радиуса 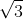   с центром $O$, лежащей в π. Пусть прямая $XM$ второй раз пересекает Ω в точке $W$ (если $XM$ касается Ω, то точки $X$ и $W$ совпадают), а прямая $OM$ пересекает Ω в точках $P$ и $Q$. Тогда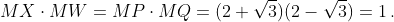  

  Пусть $YN$ – высота треугольника $XYZ$. Прямая $YN$ пересекает прямую $XM$ в ортоцентре $H$. Заметим, что прямоугольные треугольники $HYM$ и $YXM$ подобны, так что $MH : MY = MY : MX$.  Поскольку  $MY$ = 1,  то  $MX·MH$ = 1.  Поэтому  $MH = MW$,  а так как обе точки $H$ и $W$ лежат на луче $MX$, они совпадают. Таким образом, $H$ лежит на Ω.

Ответ задачи отсутствует