Заметим, что прямые $PQ$ и $MN$ пересекаются в середине $K$ отрезка $AL$. Кроме того, точка $P$ является серединой дуги $AL$ окружности $ABL$, следовательно, $\angle BPL=\angle CAL=\angle BIC-\pi/2$, где $I$ – центр вписанной окружности треугольника $ABC$, т.е. $PL\perp CI$. Аналогично $QL\perp BI$. Таким образом, стороны треугольника $PQL$ параллельны сторонам треугольника, образованного точками касания сторон треугольника $ABC$ с вписанной окружностью, а значит, касательные в этих точках к окружности $PQL$ параллельны сторонам $ABC$. Поскольку окружность $APQ$ симметрична окружности $LPQ$ относительно $PQ$, то касательная к этой окружности в точке $P$ параллельна $AB$, а касательная в точке $A$ совпадает с касательной к окружности $ABC$. При этом $\angle PAQ=\angle PLQ=\pi-\angle PIQ$, поэтому точка $I$ лежит на окружности $APQ$, а касательная к окружности в этой точке параллельна $BC$. Обозначим точку пересечения касательных в точках $A$ и $I$ через $T$.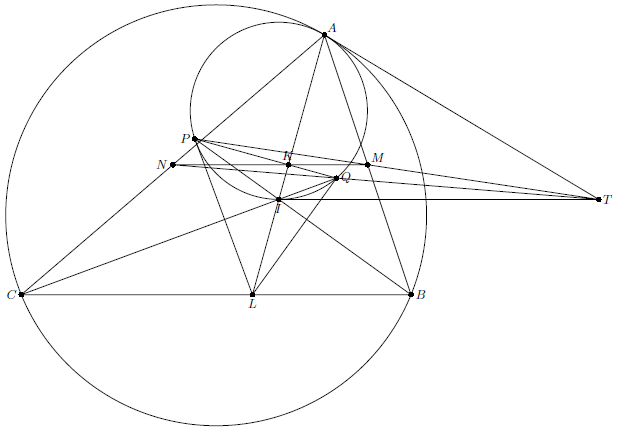Для решения задачи достаточно доказать, что прямая $PM$ проходит через $T$, т.е. что прямая, проходящая через $A$, параллельная касательной к окружности в точке $P$, и прямая , проходящая через проекцию $K$ точки $P$ на $AI$, параллельная касательной в точке $I$, пересекают $AT$ в одной точке. Пусть $S$ – точка пересечения касательных к окружности в точках $A$ и $P$, а $U$ – точка пересечения $AI$ с прямой, проходящей через $P$ и параллельной $IT$. Тогда $IK:KU=AT:AS=\operatorname{ctg}\angle IPA:\operatorname{ctg}\angle AIP$, откуда и следует искомое утверждение.

Ответ задачи отсутствует