Решение 1:Воспользовавшись формулой $r=4R\sin(A/2)\sin(B/2)\sin(C/2)$, получаем $$ \frac{r}{R}=2\sin\frac{C}2\big(\cos\frac{B-A}2-\cos\frac{A+B}2\big)<2\sin\frac{C}2\big(\frac1{\sqrt{2}}-\sin\frac{C}2\big)\leq 2\big(\frac1{2\sqrt{2}}\big)^2=\frac14. $$

Решение 2:Пусть в треугольнике $ABC$ угол $A$ – наименьший, $B$ – наибольший, $O$ – центр описанной окружности, $L$ – середина дуги $AB$, $CD$ и $PQ$ – хорда и диаметр окружности, параллельные $AB$. Так как $\smile{CD}= \smile{ADC}-\smile{AD}=\smile{ADC}-\smile{BC}>\pi$, точки $A$, $B$, $C$ лежат по одну сторону от $PQ$, т.е. $\angle OLC>\pi/4$ и расстояние от $O$ до прямой $LC$, проходящей через центр $I$ вписанной окружности больше, чем $R/\sqrt{2}$. Следовательно, $OI^2=R^2-4Rr>R^2/2$, что равносильно искомому неравенству.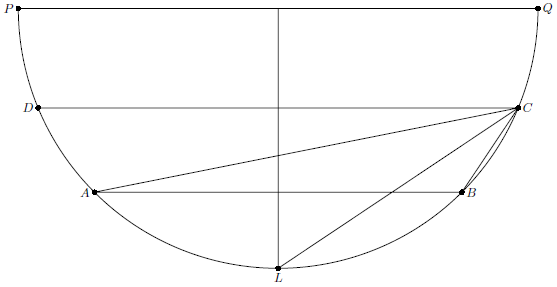

Ответ задачи отсутствует