Задача
В остроугольном треугольнике $ABC$ $CM$ – медиана, $P$ – проекция ортоцентра $H$ на биссектрису угла $C$. Докажите, что $MP$ делит отрезок $CH$ пополам.
Решение
Пусть $E$ – середина $CH$. Тогда $CE=EH=EP$ и $\angle PEH=2\angle PCH=|\angle A-\angle B|$. Но точки $E$ и $M$ лежат на окружности девяти точек, поэтому $\angle MEH=\angle MND=|\angle A-\angle B|$, где $N$ – середина $BC$, а $D$ – основание высоты из $C$.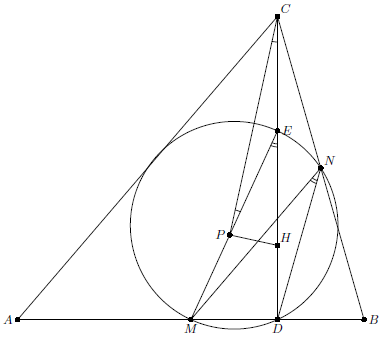
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет