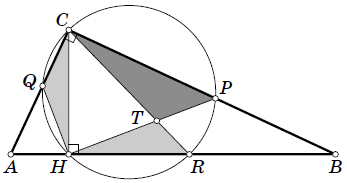
Решение 1:Добавим к рассматриваемым площадям площадь треугольника $PTR$. Получим, что нужно проверить равенство $$S_{CQH} + S_{HPR} = S_{CPR}.$$ Поскольку $\angle CHR = 90^\circ$, то $CR$ – диаметр проведённой окружности, откуда $\angle CQR = \angle CPR = 90^\circ$. В четырёхугольнике $CPRQ$ три угла прямые, поэтому он является прямоугольником.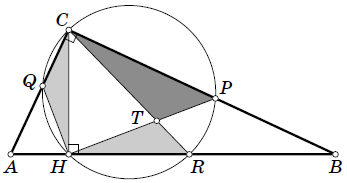Опустим из точки $H$ перпендикуляры $HX$ и $HY$ на прямые $CQ$ и $PR$ соответственно. Сумма их длин равна длине стороны $CP$ прямоугольника. Следовательно, \begin{align*} S_{CQH} + S_{HPR} &= \frac{HX \cdot CQ}{2} + \frac{HY \cdot PR}{2} = \ &= \frac{(HX + HY) \cdot PR}{2} = \ &= \frac{XY \cdot PR}{2} = \frac{CP \cdot PR}{2} = S_{CPR}. % \qedhere \end{align*}

Решение 2:Добавим к рассматриваемым площадям площадь четырёхугольника $BPTR$. Получим, что нужно проверить равенство $$S_{CQH} + S_{BPH} = S_{BRC}.$$ Из вписанности $CPRH$ следует, что $\angle PHR = \angle PCR$. Поскольку $PQ$ – диаметр окружности, то $\angle PHQ = 90^\circ = \angle CHB$, поэтому $$\angle CHQ = \angle PHR = \angle PCR.$$ Каждый из углов $HCQ$ и $CBH$ дополняет угол $BCH$ до $90^\circ$, поэтому $$\angle HCQ = \angle PBH = \angle RBC.$$ Следовательно, треугольники $CQH$, $BPH$ и $BRC$ подобны по двум углам. Тогда площади этих треугольников относятся как квадраты коэффициентов подобия, поэтому \begin{align*} S_{CQH} + S_{BPH} &= \left( \frac{CH}{BC} \right)^2 !\cdot S_{BRC} + \left( \frac{BH}{BC} \right)^2 !\cdot S_{BRC} = \ &= \frac{CH^2 + BH^2}{BC^2} \cdot S_{BRC} = S_{BRC}. \end{align*}

Они равны.