Пусть каждый отрезаемый кусочек составляет долю $(1 - a)$ куска, от которого его отрезают, $0 < a < 1$. Тогда $k$-й отрезанный кусочек составляет долю $(1 - a) a^{k-1}$ от изначального куска. Сократив на $(1 - a)$, получим, что задачу можно переформулировать следующим образом: для некоторого $a \in (0; 1)$ и натурального $n$ необходимо разбить числа $1, a, a^2, \ldots, a^{n-1}$ на три группы с равными суммами. Выберем в качестве $a$ корень уравнения $$1 = x + x^3 ; \Leftrightarrow ; 1 - x = x^3.$$ Он существует и принадлежит интервалу $(0, 1)$, потому что графики функций $y_1(x) = 1-x$ и $y_2(x) = x^3$ пересекаются внутри единичного квадрата на координатной плоскости (см. рисунок).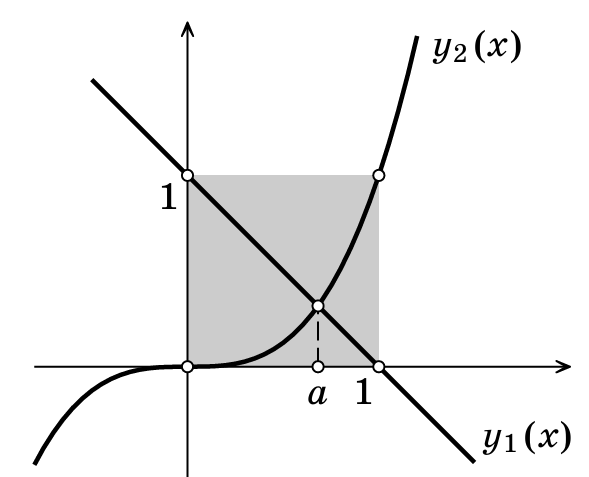Поскольку $1 = a + a^3$, то для любого натурального $k$ выполнено равенство $a^{k} = a^{k + 1} + a^{k + 3}$. Тогда $$ \begin{aligned} 1 & = a + a^3 = (a^2 + a^4) +a^3 = a^2 + (a^5 + a^7) + (a^4 + a^6) =\ &= a^2 + a^4 + a^5 + a^6 + a^7. \end{aligned} $$ Таким образом, для $n = 8$ и указанного $a$ числа 1, $a$, $\ldots$, $a^7$ можно разбить на три группы с равными суммами: $${ 1 }, \quad { a, a^3 }, \quad { a^2, a^4, a^5, a^6, a^7 }.$$

Да, может.