Решение 1:Пусть рёбра $S A, S B, S C$ параллельны граням $B C R, A C R$ и $A B R$ соответственно. Проведём через $S A$, $S B$, $S C$ плоскости, которые параллельны $B C R$, $A C R$ и $A B R$ соответственно. Получается параллелепипед, пять вершин которого совпадают с вершинами наших пирамид (рис. 1). Пусть $V$ – объём этого параллелепипеда. Тогда объём пирамиды $R A B C$ равен $V / 6$, как и объём трёх других пирамид, основаниями которых являются грани тетраэдра $S A B C$. Поэтому объём пирамиды $S A B C$ равен $V-4 \cdot V / 6=2 \cdot V / 6$, то есть вдвое больше объёма пирамиды $R A B C$, что и требовалось доказать.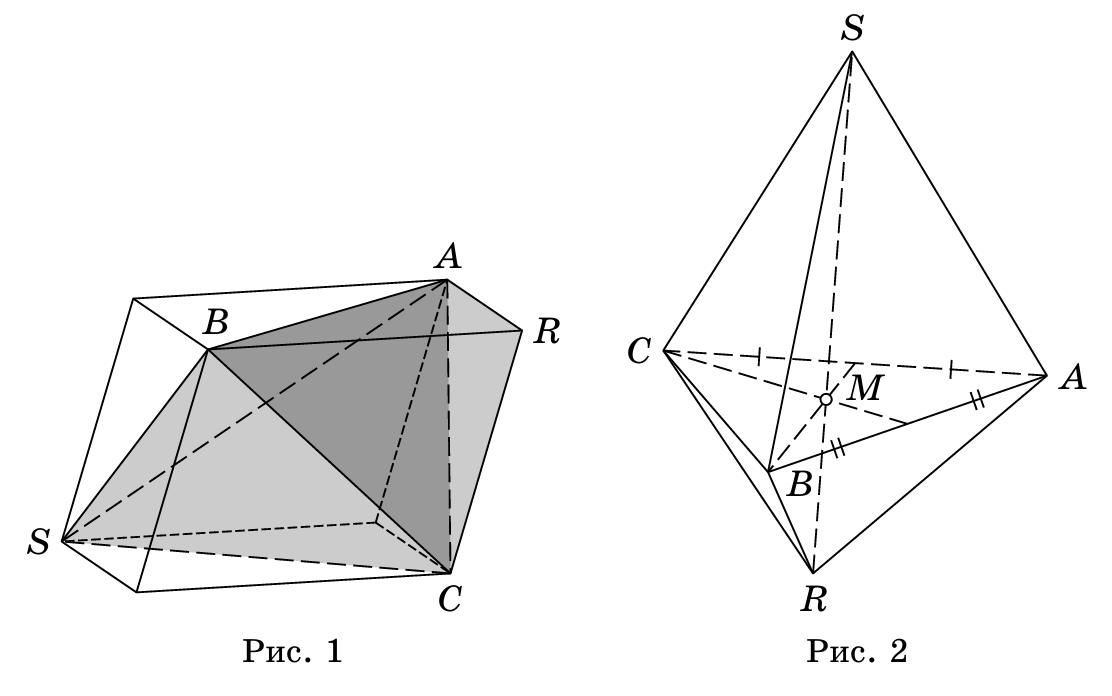

Решение 2:Пусть $M$ – точка пересечения медиан треугольника $A B C$ (рис. 2). Пусть $\alpha$, $\beta$, $\gamma$ – плоскости, проходящие через точки $A, B, C$, параллельные плоскостям $B C R, A C R, A B R$, соответственно. Поскольку $S A \parallel B C R$, точка $S$ лежит в плоскости $\alpha$. Аналогично, она лежит и в плоскостях $\beta$ и $\gamma$. Пусть $R'$ – образ точки $R$ при гомотетии с центром в точке $M$ и коэффициентом $-2$. При этой гомотетии середина отрезка $B C$ переходит в $A$, поэтому плоскость $B C R$ переходит в плоскость $\alpha$. Значит, $R' \in \alpha$. Аналогично, $R' \in \beta$ и $R' \in \gamma$. Плоскости $A B R$, $B C R$, $A C R$ имеют единственную общую точку, поэтому их образы $\alpha$, $\beta$, $\gamma$ при рассматриваемой гомотетии тоже имеют единственную общую точку. Таким образом, получаем, что $R'=S$. По построению точки $R'$ расстояние от неё до плоскости $A B C$ в два раза больше, чем расстояние от $R$ до этой плоскости, поэтому объём пирамиды $R' A B C$ (она же $S A B C$) вдвое больше объёма пирамиды $R A B C$.

Ответ задачи отсутствует