Задача
|
а) Пусть |
Решение
а) Обозначим площадь треугольника с вершинами X, Y, Z через s(XYZ). Пользуясь тем, что отношение треугольников с одинаковыми высотами (или с одинаковыми основаниями) равно отношению оснований (соответственно отношению высот), нетрудно доказать, что
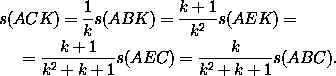
s(ALB)=s(CMB)=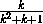 s(ABC).>
s(ABC).>
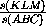 = 1 -
= 1 - 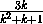 =
= 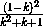 =
=
 .
.
б) Заметим, что при k = 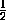 это отношение равно
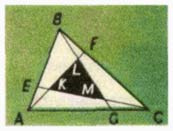
это отношение равно 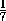 и каждый из трех отрезков AF , BG , CE разбит двумя другими в отношении3 : 3 : 1, так что если провести через точки M, K, L еще три прямые,
соответственно параллельные этим отрезкам, то каждая из сторон
треугольника ABC будет разбита в отношении2 : 1 : 1 : 2.
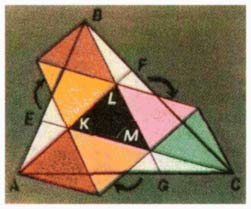
Теперь уже нетрудно из13кусков, на которые разрезан треугольник ABC,
собрать7равных треугольников (один из них состоит из единственного
куска KLM ; рис. ниже).
и каждый из трех отрезков AF , BG , CE разбит двумя другими в отношении3 : 3 : 1, так что если провести через точки M, K, L еще три прямые,
соответственно параллельные этим отрезкам, то каждая из сторон
треугольника ABC будет разбита в отношении2 : 1 : 1 : 2.
Теперь уже нетрудно из13кусков, на которые разрезан треугольник ABC,
собрать7равных треугольников (один из них состоит из единственного
куска KLM ; рис. ниже).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь