Решим задачу для n дуг. Обозначим сумму длин n дуг, образующих множество F через S (Поскольку нас интересует только относительная длина дуг, мы будем измерять ее в градусах.) .

S может быть сколь угодно близко к 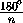. Достаточно привести пример: располагаем (n-1) дугу, длина каждой из которых равна 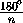так, чтобы центры любых двух соседних отстояли на 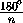, а за (n-1)-й помещаем n -ю дугу с длиной 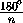так, чтобы расстояние между их ближайшими концами равнялось .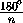

Легко проверяется, что указанная система дуг удовлетворяет условию задачи. При соответствующем выборе a₀ сумма длин дуг будет как угодно близка к .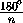

Если же точку на окружности считать дугой нулевой длины, то, заменив в примере все дуги, кроме последней, на точки, получаем множество F с суммой длин дуг, равной 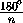(рис.1).

Докажем, что сумма S длин дуг не может быть меньше этого числа. Представим себе, что мы имеем два экземпляра нашей окружности, на которых размещены те же самые n дуг. Повернем одну из окружностей на угол ϕ , 0< ϕ<360^o . Рассмотрим множество U_ij всех таких значений ϕ , для которых при таком повороте i -я дуга повернутой окружности пересекается с j -й дугой неподвижной окружности. Нарисуем отдельно "контрольную" окружность (с выбранной на ней начальной точкой ϕ=0 (рис.2)) и отметим на ней множества U_ij для всех i, j от 1 до n . Ясно, что U_ij является дугой с длиной, равной сумме длин i -й и j -й дуг.

Отмеченные множества U_ij должны заполнять всю "контрольную" окружность, так как при любом повороте какие-то две дуги нашего множества должны пересекаться, поэтому сумма длин всех U_ij не меньше 360^o . С другой стороны, эта сумма равна 2n · S , так как каждая дуга множества входит в сумму 2n раз.

Отсюда получаем, что S 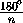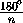= 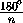. Нетрудно заметить, что неравенство должно быть строгим (если отдельные точки не считать дугами), так как любые две области U_ii и U_jj имеют общий участок, содержащий начало отсчета.

Ответ задачи отсутствует