Задача
Из последовательности a, a + d, a + 2d, a + 3d, ..., являющейся бесконечной арифметической прогрессией, где d не равно 0, тогда и только тогда можно выбрать подпоследовательность, являющуюся бесконечной геометрической прогрессией, когда отношение a/d рационально. Докажите это.
Решение
Очевидно, можно считать, что a и d одного знака.
1) Пусть a/d рационально, то есть равно s/r , где s и r – натуральные числа (случай a = 0 очевиден). При любом натуральном m число
(1 + r)m – 1 делится на (1 + r) – 1 = r, поэтому число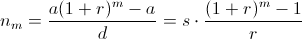 
– натуральное. Следовательно, каждый член геометрической прогрессии a(1 + r)m, (m = 0, 1, 2, ...) имеет вид a(1 + r)m = a + nmd, то есть принадлежит арифметической прогрессии.
2) Пусть арифметическая прогрессия a + nd (d ≠ 0) содержит хотя бы три последовательных члена геометрической прогрессии: a + kd, a + ld,
a + md (k < l < m). Тогда (a + ld)² = (a + kd)(a + md), откуда a(2l – k – m) = d(km – l²).
Если 2l – k – m = 0, то km – l² = 0. Но тогда (k – m)² = (k + m)² – 4km = 4l² – 4l² = 0 и, следовательно, k = m, что неверно.
Поэтому число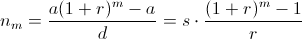 
рационально.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь