Задача
а) x1, x2, x3, x4, x5 – положительные числа. Докажите, что квадрат суммы этих чисел не меньше учетверённой суммы произведений x1x2, x2x3, x3x4, x4x5 и x5x1.
б) При каком наибольшем cn для любых неотрицательных x1, ..., xn верно неравенство (x1 + x2 + ... + xn)² ≥ cn(x1x2 + x2x3 + ... + xnx1)
(в правой части n слагаемых)?
Решение
а) Обозначим p = x1x2 + x2x3 + x3x4 + x4x5 + x5x1.
Если x2 ≥ x1, то (x1 + x2 + x3 + x4 + x5)² – (x1 – x2 + x3 – x4 + x5)² = (2x1 + 2x3 + 2x5)(2x2 + 2x4) = 4p + 4x1x4 + 4x5(x2 – x1) > 4p.
Если x2 ≤ x1, то аналогично (x1 + x2 + x3 + x4 + x5)² – (x2 – x1 + x3 – x4 + x5)2 = 4(x2 + x3 + x5)(x1 + x4) = 4p + 4x2x4 + 4x3(x1 – x2) > 4p.
В обоих случаях (x1 + x2 + x3 + x4 + x5)² > 4p. При n = 2 неравенство (x1 + x2)² ≥ 2(x1x2 + x2x1) очевидно. С другой стороны, подставив x1 = x2 = 1, получаем 4 ≥ 2c2, то есть c2 ≤ 2.
При n = 3 неравенство (x1 + x² + x3)² ≥ 3(x1x2 + x2x3 + x3x1) сводится к известному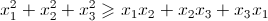 
(см. задачу 130865). С другой стороны, подставив x1 = x2 = x3 = 1, получаем 9 ≥ 3c3, то есть c3 ≤ 3.
При n ≥ 4, подставив x1 = x2 = 1, x3 = x4 = ... = xn = 0, получим 4 ≥ cn.
Докажем неравенство (x1 + ... + xn)² ≥ 4(x1x2 + x2x3 + ... + xnx1) по индукции.
База (n = 4). (x1 + x2 + x3 + x4)² – 4(x1x2 + x2x3 + x3x4 + x4x1) = ((x1 + x3) + (x2 + x4))² – 4(x1 + x3)(x2 + x4) = ((x1 + x3) – (x2 + x4))² ≥ 0.
Шаг индукции. Можно считать, что xn+1 – наименьшее из чисел x1, ..., xn+1. Тогда
(x1 + ... + xn+1)² ≥ (x1 + ... + xn)² + 2xn+1(x1 + ... + xn) + (xn+1)² ≥ 4(x1x2 + x2x3 + ... + xnx1) + 2xn+1(x1 + xn) + (xn+1)² =
= 4(x1x2 + x2x3 + ... + xn+1x1) + 4xnx2 – 2xnxn+1 – 2xnxn+1 + (xn+1)² = 4(x1x2 + x2x3 + ... + xn+1x1) + (2x1 – xn+1)(2xn – xn+1) ≥
≥ 4(x1x2 + x2x3 + ... + xn+1x1).
Ответ
б) c2 = 2, c3 = 3, cn = 4 при n ≥ 4.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь