Задача
Решить систему: 10x1 + 3x2 + 4x3 + x4 + x5 = 0, 11x2 + 2x3 + 2x4 + 3x5 + x6 = 0, 15x3 + 4x4 + 5x5 + 4x6 + x7 = 0, 2x1 + x2 – 3x3 + 12x4 – 3x5 + x6 + x7 = 0, 6x1 – 5x2 + 3x3 – x4 + 17x5 + x6 = 0, 3x1 + 2x2 – 3x3 + 4x4 + x5 – 16x6 + 2x7 = 0, 4x1 – 8x2 + x3 + x4 – 3x5 + 19x7 = 0.
Решение
Запишем уравнения системы в виде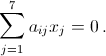 
Коэффициенты aij обладают следующим свойством: 
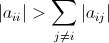для каждого i. Пусть x1, ..., x7 – ненулевое решение рассматриваемой системы, и xk – наибольшее по абсолютной величине из этих чисел. Тогда 
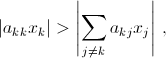поэтому равенство 
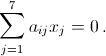не может выполняться. Противоречие.
Ответ
(0, 0, 0, 0, 0, 0, 0).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет