Решение системы с многочленами и делимостью — олимпиадная задача 9-11
Задача
Найти все действительные решения системы 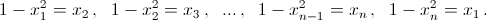
Решение
Рассмотрим последовательность, заданную первым членом x1 и рекуррентной формулой xk+1 = f(xk), где f(x) = 1 – x². Нам нужно узнать, при каких x1 последовательность будет периодической. Заметим, что функция f имеет две неподвижные точки (два решения уравнения f(x) = x):  Поэтому при x1 = a и x1 = b последовательность будет постоянной. Кроме того, f имеет две точки периода 2:
Поэтому при x1 = a и x1 = b последовательность будет постоянной. Кроме того, f имеет две точки периода 2:
f(0) = 1, f(1) = 0. Поэтому при x1 = 0 и x1 = 1 последовательность имеет период 2. Докажем, что при других значениях x1 последовательность периодической не будет.
Заметим, что а) f(x) ≤ 1 при всех x; б) f(x) > 0 при –1 < x < 1; в) f(x) < x при x < a и x > b; г) f(x) > x при a < x < b; д) f(x) > b при
0 < x < b, f(x) < b при b < x < 1. Разберём несколько случаев.
1) x1 > 1. В силу а) ни один из следующих членов последовательности не равен x1.
2) x1 < a. В силу в) x2 < x1 < a, x3 < x2 < a, ..., то есть последовательность убывает. Следовательно, она непериодическая.
3) a < x1 < 0. Пока члены последовательности находятся в этом интервале, в силу г) выполнено неравенство xk+1 > xk, то есть последовательность возрастает. Если последовательность никогда не покинет этот интервал (на самом деле это невозможно, но мы не будем тратить время на доказательство), то она непериодическая. Если же какой-то член xk ≥ 0, то силу а) и б) все последующие члены находятся на отрезке [0, 1], и ни один из них не равен x1.
4) 0 < x1 < b. Тогда в силу д), а) и б) все нечётные члены находятся в интервале (0, b), а все чётные – в интервале (b, 1). Докажем, что последовательность нечётных членов убывает. Для этого достаточно проверить, что f(f(x)) = 1 – (1 – x²)² < x при 0 < x < b.
Действительно, x – 1 + (1 – x²)² = x(x – 1)(x² + x – 1) > 0 (первый множитель на указанном интервале положителен, а два других отрицательны). Таким образом, последовательность непериодична.
5) b < x1 < 1. Тогда все чётные члены находятся в интервале (0, b), и, как показано выше последовательность чётных членов убывает. Таким образом, и в этом случае последовательность непериодична.
Ответ
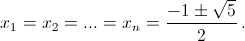
При чётном n добавляются еще два решения: (0, 1, 0, 1, ..., 0, 1) и (1, 0, 1, 0, ..., 1, 0).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь