Задачи и олимпиады по математике

Задача

Играют двое; один из них загадывает набор из целых чисел (x₁,x₂,...,x_n) -- однозначных, как положительных, так и отрицательных. Второму разрешается спрашивать, чему равна суммаa₁x₁+ ... +a_nx_n, где(a₁...a_n) -- любой набор. Каково наименьшее число вопросов, за которое отгадывающий узнает задуманный набор?

Решение

Покажем, что задуманный набор можно определить, задав всего один вопрос. Именно, достаточно взять

a₁ = 100, a₂ = 100²,..., a_n = 100ⁿ.

Тогда сообщённая нам сумма равна

S₁ = 100x₁ + 100²x₂ + ... + 100ⁿx_n.

Рассмотрим теперь соотношение

$\displaystyle {\frac{S_{1}}{100^{n}}}$ = $\displaystyle {\frac{100x_{1}+100^{2}x_{2}+\dots +100^{n-1}x_{n-1}}{100^{n}}}$ + x_n

и покажем, что

$\displaystyle \Bigl\vert$$\displaystyle {\frac{100x_{1}+100^{2}x_{2}+\dots +100^{n-1}x_{n-1}}{100^{n}}}$$\displaystyle \Bigr\vert$ < $\displaystyle {\textstyle\frac{1}{10}}$.

Действительно,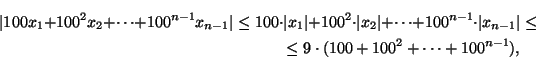

$\begin{multline*} \vert 100x_{1}+100^{2}x_{2}+\dots +100^{n-1}x_{n-1}\vert\le 1... ... x_{n-1}\vert\le\\ \le 9\cdot (100+100^{2}+\dots +100^{n-1}), \end{multline*}$

так какx₁,x₂, ...,x_{n - 1} — однозначные числа. Число9(100 + 100²+ ... + 100^{n - 1}), как легко понять, имеет 2n- 1 десятичных знаков и состоит из нулей и девяток, т. е. оно меньше, чем$\underbrace{99\dots 999}_{\mbox{$, и подавно меньше, чем 10^{2n - 1}.

Таким образом, интересующее нас отношение меньше, чем

$\displaystyle {\frac{10^{2n-1}}{100^{n}}}$ = $\displaystyle {\frac{10^{2n}\cdot\frac{1}{10}}{10^{2n}}}$ = $\displaystyle {\textstyle\frac{1}{10}}$.

Мы показали, что отношение$\displaystyle {\frac{S_{1}}{100^{n}}}$отличается от целого числа х_nменьше, чем на$\displaystyle {\textstyle\frac{1}{10}}$; это, очевидно, позволяет однозначно определить х_n. Зная х_n, мы можем найти сумму

S₂ = S₁ - 100ⁿx_n = 100x₁ + 100²x₂ + ... + 100^{n - 1}x_{n - 1}

и по ней найти х_{n - 1}(разделив на 100^{n - 1}), и т. д.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления