Задача
Сеть метро имеет на каждой линии не менее 4 станций, из них не более трёх пересадочных. Ни на какой пересадочной станции не скрещиваются более двух линий. Какое наибольшее число линий может иметь такая сеть, если с каждой станции на любую другую можно попасть, сделав не больше двух пересадок?
Решение
Зафиксируем какую-нибудь линию. На ней есть неперсадочная станция. С нее, сделав одну пересадку, можно попасть не более, чем на 3 линии, а с каждой из них, сделав еще одну пересадку, – ещё не более, чем на две линии. Следовательно, всего линий не более чем 1 + 3 + 2·3 = 10. На рисунке показана схема пересадок для десяти линий, удовлетворяющая условию (для удобства беспересадочные станции не отмечены; "пересечения", не отмеченные кружочками, станциями не являются).
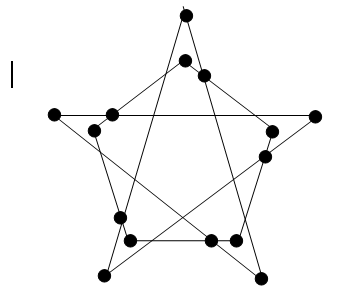
Ответ
10 линий.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь