Будем считать, что Джимми стреляет параллельно оси вертилятора, чуть выше неё. Тогда траектория пули изображается прямой с положительным угловым коэффициентом на плоскости  (x, t)  (x – координата вдоль оси, t – время). Чтобы понять, какой выстрел будет удачным, рассмотрим четыре вертикальные прямые, соответствующие абсциссам точек "крепления" полудисков (занумеруем их слева направо). По условию расстояния между соседними прямыми одинаковы. Разобьем каждую прямую на участки длины δ  (2δ = ¹/₅₀  – время оборота оси). Каждый второй участок – чёрный отрезок, остальные – белые интервалы (рис. слева). Чёрные точки соответствуют попаданию пули в данный момент в полудиск, белые – промаху. Таким образом, надо доказать, что найдется прямая с положительным угловым коэффициентом, проходящая через четыре чёрные точки.

  Возьмём на прямых №2 и №3 по чёрному отрезку, правый из которых находится целиком выше левого. Проведём прямую через верхний конец правого и нижний конец левого отрезка, а также прямую через нижний конец правого и верхний конец левого. Эти прямые пересекутся в точкеOпосередине между прямыми №2 и №3 (рис. справа). Область между этими прямыми назовёмвеером; любая прямая, проходящая через точкуOвнутри веера пересекает прямые №2 и №3 в чёрных точках.   Веер пересекает прямую №1 по отрезку длины 3δ, поэтому на прямой №1 найдётся чёрный отрезок целиком попавший в веер. Сузим веер, проведя новые прямые через точкуOи концы этого отрезка (рис. справа). Малый веер пересекает прямую №4 по отрезку длины один, поэтому это пересечение содержит чёрные точки (в худшем случае это пересечение состоит из белого интервала и двух чёрных точек на его концах). Соединив одну из этих чёрных точек сO, мы получим искомую прямую, проходящую через четыре чёрные точки.

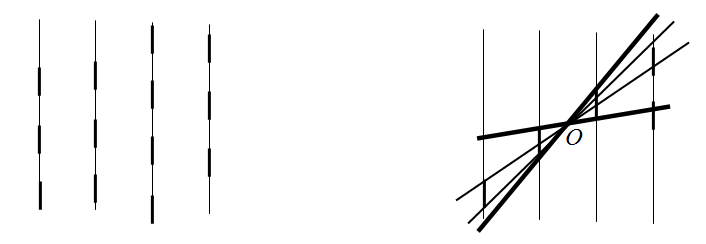
Ответ задачи отсутствует