Система уравнений с параметром k: олимпиадная задача по алгебре для 11
Задача
Рассматривается система уравнений:
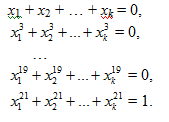
Докажите, что при некоторых k такая система имеет решение.
Решение
Рассмотрим сначала систему уравнений ![]()
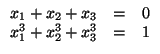 . Будем искать решение этой системы в следующем частном виде:
. Будем искать решение этой системы в следующем частном виде:
x1 = x2 = λ, x3 = μ. Для λ и μ мы получаем уравнения 2λ + μ = 0, λ3 + μ3 = 1, откуда находим μ = – 2λ и – 6λ3 = 1.
Рассмотрим затем систему уравнений ![]()
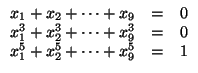 . Пусть u = (t1, t2, t3) – решение предыдущей системы. Будем искать решение новой системы в следующем виде: (x1, x2, x3) = (x4, x5, x6) = λu, (x7, x8, x9) = μu. Первое уравнение выполняется автоматически, а следующие два уравнения выполняются тогда и только тогда, когда 2λ3 + μ3 = 0 и
2λ5 + μ5 = 1, то есть μ = –
. Пусть u = (t1, t2, t3) – решение предыдущей системы. Будем искать решение новой системы в следующем виде: (x1, x2, x3) = (x4, x5, x6) = λu, (x7, x8, x9) = μu. Первое уравнение выполняется автоматически, а следующие два уравнения выполняются тогда и только тогда, когда 2λ3 + μ3 = 0 и
2λ5 + μ5 = 1, то есть μ = – ![]() λ и
λ5(2 –
λ и
λ5(2 – ![]() ) = 1.
) = 1.
Дальше мы поступаем аналогично: каждый раз добавляем одно уравнение и утраиваем число переменных. При этом для λ и μ получаем соотношения
μ = – ![]() λ и λ2k+1(2 –
λ и λ2k+1(2 – ![]() ) = 1.
) = 1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь