Пусть u и v – максимальные скорости полицейского и гангстера. Введём систему координат с началом в центре исходного квадрата ABCD и осями, параллельными его сторонам. Положим сторону квадрата ABCD равной 6 м и будем считать, что максимальная скорость гангстера  v = 3 (м/мин)  (нам ведь важно лишь отношение  u : v).  Точки, в которых находятся полицейский и гангстер, обозначим через  П(х_П, y_П)  и  Г(x_Г, y_Г),  соответственно. Обозначим через Г' точку с координатами  (⅓ x_Г, ⅓ y_Г);  если точка Г движется по контуру квадрата ABCD со скоростью 3, то Г' движется по контуру квадрата со стороной 2 со скоростью 1.   а-в) Докажем, что полицейский достигнет своей цели (то есть окажется с гангстером на одной стороне квадрата; будем говорить, что в этом случае он ловит гангстера). Полицейский будет ловить гангстера в несколько этапов.  Первый этап. Полицейский догоняет Г'. Это всегда можно сделать, так как  u> 1.  Первый этап заканчивается, когда точки П и Г' совпадают.  Второй этап. Можно считать без ограничения общности, что к концу первого этапа точка Г окажется на сторонеAВ; тогда  3x_П=x_Г.  На протяжении всего второго этапа полицейский должен двигаться таким образом, чтобы всё время выполнялось равенство  3x_П=x_Г;  для этого необходимо и достаточно, чтобы то же соотношение все время имело место для горизонтальных составляющих скоростей полицейского и гангстера. При этом по вертикали полицейский может двигаться к сторонеABсо скоростью 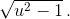   Возможны два случая.   1) Г остаётся все время наAB. Тогда П через некоторое время достигнетAB, и гангстер будет пойман.   2) В какой-то момент Г уйдёт со стороныAB. Как только Г достигнет границыAB(будем считать, точкиB) начинается  Третий этап. К началу этого этапа точки Г иBсовпадают, а точка П находится от каждой из сторонABиBCна расстоянии, не большем 2. На третьем этапе полицейский должен с максимальной скоростью приближаться по перпендикуляру к той стороне, на которой находится гангстер (если  Г находится вB,  то безразлично, к какой именно, – к сторонеABили же к сторонеBC). Чтобы добежать из точкиBдо точкиAили до точкиС, гангстеру понадобится 2 минуты, а полицейскому, чтобы достигнуть соответствующей стороны (ABилиBС), понадобится меньше 2 минут. Следовательно, полицейский поймает гангстера на одной из сторонABилиBC.   г) Покажем, что при  u = 1 м/мин   гангстер может выбрать такую стратегию, при которой полицейский не сумеет его догнать. Проведём прямые A'B', C'D', параллельные стороне AB, и прямые A"D", B"C", параллельные BC, так, чтобы  AA' = BB' = CC' = DD' = AA" = BB" = CC" = DD" = 1  (рис. слева). Пусть в самом начале гангстер Г находится в середине стороны AB, а полицейский П – над прямой A'B'. Проведём между П и A'B' вспомогательную прямую A₁B₁, параллельную AB (рис. справа).

  Опишем теперь стратегию гангстера. Пока полицейский находится выше прямойA₁B₁, гангстер остаётся на месте – в серединеAB. Рано или поздно полицейский достигнетA₁B₁(иначе он никогда не поймает гангстера).   Пусть при этом  x_П≤ 0  (случай  x_П≥ 0  симметричен). Тогда Г перебегает в середину отрезкаBC. На это ему требуется 2 минуты. За первую минуту (пока ганстер находится наAB) полицейский не успеет добежать до прямойABи, значит, не сможет поймать Г на сторонеAB. Кроме того, за 2 минуты он не успеет добежать до прямойB"C".   Итак, мы пришли к конфигурации, эквивалентной начальной: Г – в середине стороныBC, а П – левее прямойB"C". При этом прошло более 2 минут.   Дальнейшее поведение Г аналогично описанному выше. Очевидно, что при такой стратегии гангстера полицейский не поймает его ни за какое конечное время.

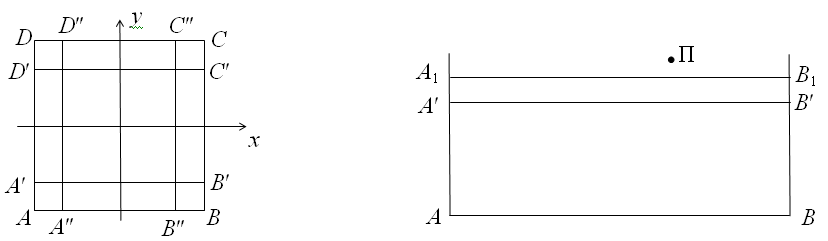
Ответ задачи отсутствует