Задача
Дано число A = 
, где n и m –
натуральные числа, не меньшие 2.
Доказать, что существует такое натуральное k, что A =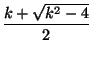 
.
Решение
Число x = является корнем квадратного уравнения
x + 
= n. Для каждого натурального m рассмотрим число km = xm + 
. Легко проверить, что
km+1 = km(x + ) – km–1 = nkm – km–1. Поэтому число km целое для любого натурального m. При этом km > 0,
xm =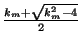 
.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет