Задачи и олимпиады по математике

Задача

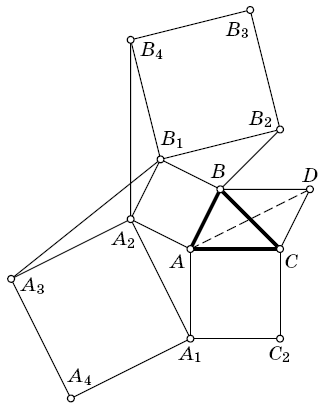
На сторонах треугольника ABC вовне построены квадраты ABB₁A₂, BCC₁B₂ и CAA₁C₂. На отрезках A₁A₂ и B₁B₂ также во внешнюю сторону от треугольников AA₁A₂ и BB₁B₂ построены квадраты A₁A₂A₃A₄ и B₁B₂B₃B₄. Докажите, что A₃B₄ || AB.

Решение

Решение 1: Поскольку AB = BB₁, BC = BB₂ и ∠B₁BB₂ = π − ∠ABC, то S_ABC = S_BB₁B₂. Аналогично, S_B₁A₂A₃ = S_AA₁A₂ = S_ABC = S_BB₁B₂ = S_B₁A₂B₄. Следовательно,

A₃B₄ || A₂B₁ || AB.

Решение 2: Заметим, что медиана треугольника ABC, проведённая из вершины A, перпендикулярна отрезку A₁A₂ и равна его половине. Действительно, если D – четвёртая вершина параллелограмма ABDC, то треугольник ABD является образом треугольника A₂AA₁ при повороте на 90° вокруг центра квадрата ABB₁A₂.

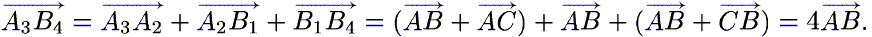
Аналогично, отрезокA₃A₂параллелен медиане треугольникаABC, проведённой из вершиныB, и вдвое длиннее её. Поэтому

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления