Задача
В квадрате со стороной 1 проведено конечное количество отрезков, параллельных его сторонам. Отрезки могут пересекать друг друга. Сумма длин проведенных отрезков равна 18. Докажите, что среди частей, на которые разбивается квадрат этими отрезками, найдётся такая, площадь которой не меньше 0,01.
Решение
Предположим противное. Пусть периметр i-й части равен Pi, а площадь – Si < 0,01. Вокруг i-й части можно описать прямоугольник с периметром не больше Pi, а среди прямоугольников с данным периметром наибольшую площадь имеет квадрат. Следовательно, Pi ≥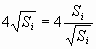 
> 40Si, значит, ∑ Pi > 40 ∑ Si = 40. С другой стороны, ∑ Pi не превосходит удвоенной суммы отрезков плюс периметр исходного квадрата, то есть 36 + 4 = 40. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь