Решение 1:Пусть d – наибольшее расстояние между вершинами четырёхугольника. Тогда весь четырёхугольник лежит в пересечении кругов радиуса d с центрами в соответствующих вершинах (пусть A и B). Эта фигура, в свою очередь, помещается в круг радиуса 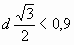   с центром в середине отрезка AB.

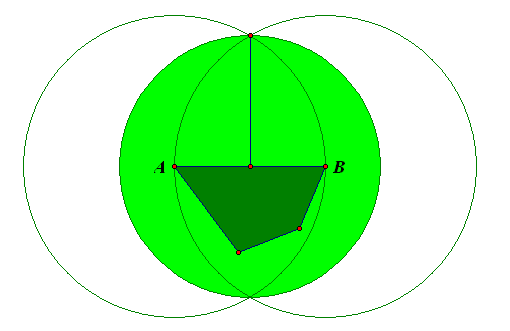
Решение 2:Проекция такого четырёхугольника на любую прямую – отрезок длины, меньшей 1. Значит, его можно заключить в квадрат со стороной 1. Описанная окружность этого квадрата имеет радиус, меньший 0,75.

Ответ задачи отсутствует