Задача
Дана бесконечная клетчатая бумага со стороной клетки, равной единице. Расстоянием между двумя клетками называется длина кратчайшего пути ладьи от одной клетки до другой (считается путь центра ладьи). В какое наименьшее число красок нужно раскрасить доску (каждая клетка закрашивается одной краской), чтобы две клетки, находящиеся на расстоянии 6, были всегда окрашены разными красками?
Решение
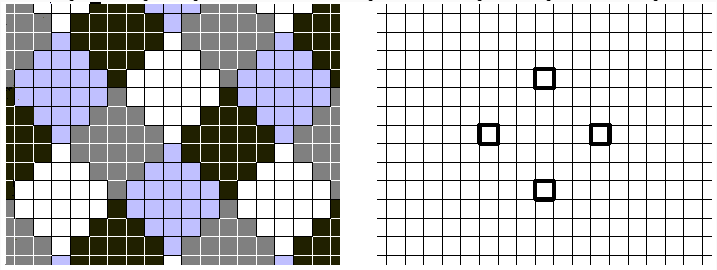
Пример раскраски клетчатой плоскости в четыре цвета, при которой каждые две клетки на расстоянии 6 окрашены в разные цвета, представлен на рис. слева.
Ответ
В 4 цвета.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет