Задача
Рассматриваются 4(N – 1) граничных клеток таблицы размером N×N. Нужно вписать в эти клетки последовательные 4(N – 1) целых чисел так, чтобы сумма чисел в вершинах любого прямоугольника со сторонами, параллельными диагоналям таблицы, в том числе и в "вырожденных" прямоугольниках – диагоналях, равнялась одному и тому же числу (для прямоугольников суммируются четыре числа, для диагоналей – два числа). Возможно ли это? Рассмотрите случаи:
а) N = 3;
б) N = 4;
в) N = 5.
Решение
а), в) На рисунках 1а, 1б приведены соответствующие расстановки.
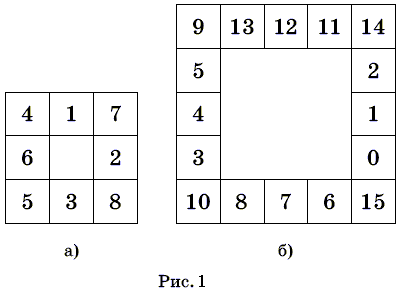
Ответ
а), в) Возможно; б) невозможно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет