Решения системы: (x + y)³ = z, (y + z)³ = x, (z + x)³ = y
Задача
Найти все решения системы уравнений: (x + y)³ = z, (y + z)³ = x, (z + x)³ = y.
Решение
Решение 1: Вычитая из первого уравнения второе, получим: (x – z)((x + y)² + (x + y)(y + z) + (y + z)²) = – (x – z).
Поскольку выражение вида a² + ab + b² не может быть отрицательным, x = z. Аналогично x = y.
Осталось решить уравнение (2x)³ = x.
Решение 2:В силу симметрии системы уравнений можем считать, что x ≥ y. Тогда (y + z)³ = x ≥ y = (z + x)3, поэтому y + z ≥ z + x, то есть y ≥ x. Значит, x = y. Аналогично y = z.
Ответ
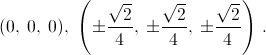
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет