Олимпиадная задача: прямоугольники в квадрате, доказательство о площад
Задача
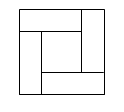 Квадрат разбит на пять прямоугольников так, что четыре угла квадрата являются углами четырёх прямоугольников, площади которых равны между собой, а пятый прямоугольник не имеет общих точек со сторонами квадрата. Докажите, что этот пятый прямоугольник есть квадрат.
Квадрат разбит на пять прямоугольников так, что четыре угла квадрата являются углами четырёх прямоугольников, площади которых равны между собой, а пятый прямоугольник не имеет общих точек со сторонами квадрата. Докажите, что этот пятый прямоугольник есть квадрат.
Решение
Рассмотрим наименьшую из сторон "угловых" прямоугольников. Тогда его вторая сторона является наибольшей. Но также наибольшей является сторона соседнего прямоугольника (дополняющая наименьшую сторону до стороны исходного квадрата). Поэтому эти прямоугольники равны. Отсюда, очевидно, следует равенство всех "угловых" прямоугольников.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет