Задачи и олимпиады по математике

Задача

Дан выпуклый четырёхугольник и точка M внутри него. Доказать, что сумма расстояний от точки M до вершин четырёхугольника меньше суммы попарных расстояний между вершинами четырёхугольника.

Решение

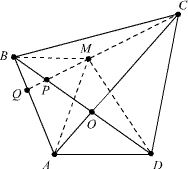
Пусть диагонали AC и BD пересекаются в точке O. Без ограничения общности можно считать, что M лежит в треугольнике BOC. Пусть прямая CM пересекает сторону AB в точке Q.

Согласно неравенству треугольника: MB + MC ≤ BP + PM + MC = BP + PC ≤ BP + PO + OC = OB + OC, что меньше суммы диагоналей; MA + MD < AQ + QM + MC + CD = AQ + QC + CD < AQ + QB + BC + CD = AB + BC + CD, то есть меньше периметра четырёхугольника. Сложив, получим доказываемое неравенство.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления