Назад
Задача 197891 • Сложность: 2 • 10-11 класс
Задача

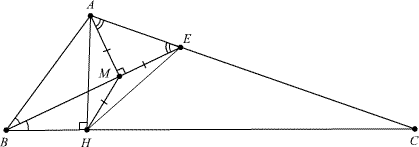
В треугольнике ABC проведены высота AH и биссектриса BE. Известно, что угол BEA равен 45°. Докажите, что угол EHC равен 45°.

Решение

  Опустим из вершины A перпендикуляр AM на BE. Треугольник AME равнобедренный прямоугольный.

  Точки M и H лежат на окружности с диаметром AB, значит,  MH = MA = ME  (на дуги AE и MH опираются равные углы). Следовательно, M – центр описанной окружности треугольника AHE, поэтому  ∠AHE = ½ ∠AME = 45°,  а  ∠EHC = 90° – ∠AHE.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет