Задача
Докажите, что при любом a имеет место неравенство: 3(1 + a² + a4) ≥ (1 + a + a²)².
Решение
Решение 1:1 + a² + a4 = (1 + a²)² – a². Поэтому неравенство можно сократить на 1 + a + a² > 0. Получаем 3(1 – a + a²) ≥ 1 + a + a² ⇔ (a – 1)² ≥ 0.
Решение 2:2(1 + a + a²) ≤ 2(1 + a²) + (1 + a²), поэтому
4(1 + a + a²) ≤ (3(1 + a²))² = 9(1 + 2a² + a4) = 9(1 + a² + a4) + 9a² ≤ 9(1 + a² + a4) + 3(1 + a4) + 3a² = 12(1 + a² + a4).
Решение 3:Раскрыв скобки, приведём неравенство к виду 2(a³ – 1)(a – 1) ≥ 0.
Решение 4:Записав неравенство в виде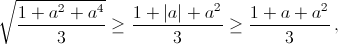 
видим, что это частный случай неравенства между средним квадратичным и средним арифметическим.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет