Олимпиадная задача по теории графов и стереометрии: минимальное число точек на додекаэдре и икосаэдре

  а) Поскольку у додекаэдра 12 граней и каждая его вершина принадлежит трём из них, искомый минимум не меньше 4. На рис. слева показано, как отметить четыре вершины.

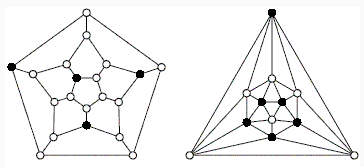
  Докажем, что меньшим числом обойтись нельзя. 12 вершин икосаэдра разбиваются на шесть пар противоположных. Если в каждой пары отмечена хотя бы одна вершина, то это уже шесть точек. Допустим, что ни одна из пары (A, B) противоположных вершин не отмечена. Тогда требуется не менее трёх вершин, чтобы "обслужить" пять граней, прилегающих к A, и еще три – для граней вокруг B.

а) 4 точки;   б) 6 точек.