Олимпиадная задача по комбинаторной геометрии для 7–9 классов от Фомина С. В.

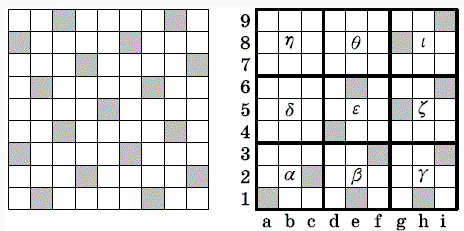
б) Предположим, что удалось закрасить 18 клеток. Разобьём квадрат 9×9 на девять квадратов 3×3. Пронумеруем клетки квадрата координатами горизонтали – буквами отaдоi, а вертикали – цифрами от 1 до 9. Квадраты 3×3 обозначим греческими буквами от α до ι, как на рисунке справа). Легко заметить, что в квадрате 3×3 может находиться не более двух закрашенных клеток,поэтому каждый из девяти квадратов 3×3 содержит ровно две закрашенные клетки. При этом из двух закрашенных клеток в квадрате 3×3 одна обязательно находится в углу. Без ограничения общности можно считать, что в центральном квадрате ε закрашена клетка d4. Тогда в квадрате α должна быть закрашена одна из угловых клеток a1, c1 или a3. Если закрашена клетка c1, в квадрате β невозможно закрасить две клетки, удовлетворяющих условиям задачи. Аналогично невозможно осуществить раскраску квадрата δ, если предположить, что закрашена клетка a3. Поэтому закрашена клетка a1. Второй закрашенной клеткой, без ограничения общности, будем считать c2. Тогда клетки, закрашенные в квадратах β и γ, определяются однозначно – e1, f3 и h1, i3. Аналогично в квадратах ζ и ι закрашенными могут быть только клетки g5, i6, g8 и i9. Вернёмся к центральному квадрату ε. Второй закрашенной клеткой в нём может быть только e6. Но тогда в квадрате θ невозможно закрасить две клетки, соблюдая условие. Противоречие.

а) См. рис. слева.