Олимпиадная задача по планиметрии: угол поворота и медианы в треугольнике, 10–11 класс
Задача
Пусть M – центр тяжести (точка пересечения медиан) треугольника ABC. При повороте на 120° вокруг точки M точка B переходит в точку P, при повороте на 240° вокруг точки M (в том же направлении) точка C переходит в точку Q. Докажите, что либо треугольник APQ – правильный, либо точки A, P, Q совпадают.
Решение
Пусть R – поворот на 60°. Заметим, что R²(a) + a = R(a) для любого вектора a. Как известно,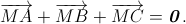 
Отсюда 
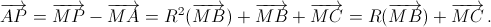Аналогично 
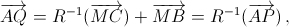что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет