Назад

Олимпиадная задача о последовательных отражениях в четырёхугольнике, 8–9 класс

Задача 198150 • Сложность: 3 • 8-9 класс
Задача

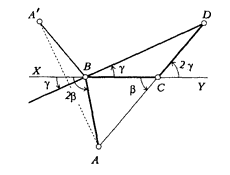
В четырёхугольнике ABCD  AB = BC = CD = 1,  AD не равно 1. Положение точек B и C фиксировано, точки же A и D подвергаются преобразованиям, сохраняющим длины отрезков AB, CD и AD. Новое положение точки A получается из старого зеркальным отражением в отрезке BD, новое положение точки D получается из старого зеркальным отражением в отрезке AC (где A уже новое), затем на втором шагу опять A отражается относительно BD (D уже новое), затем снова преобразуется D, затем аналогично проводится третий шаг, и так далее. Докажите, что на каком-то шагу положение точек совпадает с первоначальным.

Решение

  Ломаная ABCD определяется заданием двух углов:  ∠BCA = β  и  ∠CDB = γ;  при этом, если обозначить через X и Y точки на продолжениях отрезка BC, то (поскольку треугольники ABC и BCD равнобедренные, см. рисунок)  ∠XBA = 2β,  a  ∠YCD = 2γ.  Углы будем считать направленными, скажем, против часовой стрелки.

  При отражении точкиAуголXBA, равный 2β, заменяется на уголXBA', равный  γ – (2β – γ) = 2(γ – β),  (A'– это новое положение точкиA), а угол γ при точкеCне меняется. Таким образом, пара углов, задающая нашу ломаную, преобразуется так:  (β, γ)  →  (γ – β, γ).  Следующее преобразование будет точно таким же, только "первый" и "второй" меняются ролями. Продолжая чередовать такие операции, получим (β, γ)  →  (γ – β, γ)  →  (γ – β, – β)  →  (– γ, – β)  →  (– γ, β – γ)  →  (β, β – γ)  →  (β, γ)   – мы вернулись на место через 6 шагов!
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет