Олимпиадная задача: Геометрическое место точек внутри куба, равноудалённых от рёбер

  Расположим систему координат так, чтобы вершины куба ABCDA'B'C'D' имели координаты:  A(0, 0, 0),  B(1, 0, 0),  D(0, 1, 0),  A'(0, 0, 1).

  Расстояние от точки  M(x, y, z)  до ребра  a = BB'  равно расстоянию от её проекции  M'(x, y) на плоскость xOy до точки  B(1, 0),  то есть равно 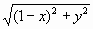  .  Аналогично квадраты расстояний от M до рёбер  b = CD  и  c = A'D'  равны, соответственно,  (1 – y)² + z²,  (1 – z)² + x².  При  x = y = z  точка M, очевидно, равноудалена от  a, b, c.  Докажем, что больше таких точек нет. Пусть не все координаты точки M равны между собой, и x – наименьшая из них, а z – наибольшая (остальные случаи разбираются точно так же). Тогда  x < z,  1 – z ≤ 1 – y   ⇔   (1 – z)² + x² < (1 – y)² + z²,  и  M не равноудалена от рёбер b и c.  Итак, искомое ГМТ – множество точек, координаты которых удовлетворяют соотношению  x = y = z.  Это диагональ AC' куба.

Большая диагональ куба, не имеющая общих точек с рёбрами  a, b, c.