Олимпиадная задача по математике на неравенства и делимость для 8-10 классов
Задача
а) Докажите для всех n > 2 неравенство 
б) Найдите какие-нибудь такие натуральные числа a, b, c, что для всех n > 2 
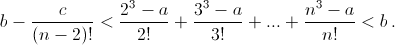
Решение
а) Заметим, что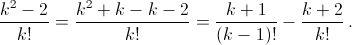 
Имеем: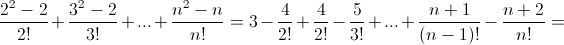 
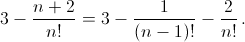
Это число, очевидно, удовлетворяет требуемым неравенствам при n > 2. б) По аналогии с пунктом а) постараемся представить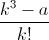 
в виде 
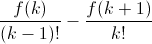(тогда снова сократятся все члены суммы, кроме первого и последнего). f(k) будем искать в виде квадратного трёхчлена f(k) = k² + pk + q. Получим соотношение
k³ – a = k(k² + pk + q) – ((k + 1)² + p(k + 1) + q) = k³ + (p – 1)k² + (q – 2 – p)k – (1 + p + q). Отсюда p = 1, q = 3, a = 5. Итак,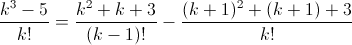 
и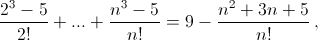 
то есть
b = 9. Осталось подобрать c так, чтобы при n > 2 выполнялось неравенство 
или n² + 3n + 5 < cn(n – 1).
Подходит, например, c = 4.
Ответ
б) Например, a = 5, b = 9, c = 4.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь