Назад

Олимпиадная задача по планиметрии для 8–9 классов от Гальперина и Васильева

Задача 198335 • Сложность: 2 • 8-9 класс
Задача

F – выпуклая фигура с двумя взаимно перпендикулярными осями симметрии. Через точку M, лежащую внутри фигуры и отстоящую от осей на расстояния a и b, провели прямые, параллельные осям. Эти прямые делят F на четыре области. Найдите разность между суммой площадей большей и меньшей из областей и суммой площадей двух других.

Авторы:
Гальперин Г. А. Васильев Н. Б.
Разделы:
Планиметрия
Источники:
Турнир городов 18 турнир (1996/1997 год) весенний тур, тренировочный вариант, 8-9 класс Олимпиады и турниры
Количество версий:
4
Решение

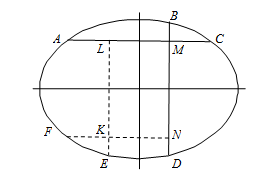
Отразив область CMD (см. рис.) относительно вертикальной оси симметрии, а область AMB – относительно горизонтальной, мы наложим их на большую область AMD.

При этом останется непокрытым прямоугольникKLMN, а участокEKF(в силу симметрии равный меньшей областиBMC) будет покрыт дважды. Поэтому (SAMD + SBMC) – (SAMB + SCMD) =SKLMN= 4ab.
Ответ

4ab.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет