Олимпиадная задача по комбинаторной геометрии о треугольных плитках для 6–8 классов
Задача
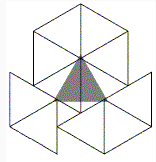
На плоскости нарисован чёрный равносторонний треугольник. Имеется девять треугольных плиток того же размера и той же формы. Нужно положить их на плоскость так, чтобы они не перекрывались и чтобы каждая плитка покрывала хотя бы часть чёрного треугольника (хотя бы одну точку внутри него). Как это сделать?
Решение
На самом деле, можно положить даже 11 плиток, так чтобы они удовлетворяли условию задачи (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет