Назад

Олимпиадная задача Шаповалова: диагонали и площадь разрезанного треугольника

Задача 198444 • Сложность: 2 • 8-9 класс
Задача

Бумажный прямоугольный треугольник перегнули по прямой так, что вершина прямого угла совместилась с другой вершиной.

  а) В каком отношении делятся диагонали полученного четырёхугольника их точкой пересечения?

  б) Полученный четырёхугольник разрезали по диагонали, выходящей из третьей вершины исходного треугольника. Найти площадь наименьшего образовавшегося куска бумаги.

Авторы:
Шаповалов А. В.
Разделы:
Планиметрия
Источники:
Турнир городов 21 турнир (1999/2000 год) осенний тур, тренировочный вариант, 8-9 класс Олимпиады и турниры
Количество версий:
5
Решение

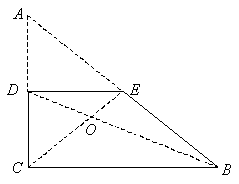
  a) Треугольник ABC перегнули, очевидно, по средней линии DE (см. рис.). Поэтому "диагонали" CE и BD были его медианами. Значит,

BO : OD = CO : OE = 2 : 1.

  б) После разреза образуется три куска. Два из них – треугольники DOC и BCD, третий составлен из треугольников DOE и BDE (после разворачивания он тоже превратится в треугольник). Наименьшая площадь у треугольника OCD (он является частью треугольника BCD, а также частью треугольника CDE, равновеликого треугольнику BDE). Поскольку  OD = ⅓ BD,  то  SOCD = ⅓ SBCD = ⅙ SBCA.
Ответ

a)  2 : 1;   б)  ⅙.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет