Олимпиадная задача по комбинаторной геометрии: разделение листа с дырками (Шаповалов А.В.)

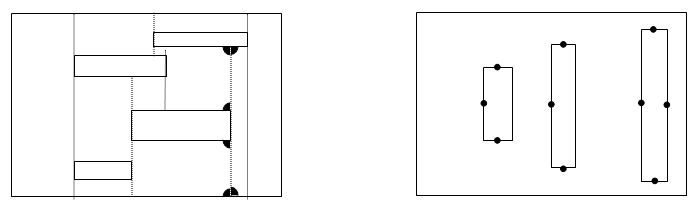
  Оценка. Будем считать, что одна из сторон листа вертикальна. Вдоль каждой вертикальной "стороны" одной из дырок проведём вертикальный разрез до "упора" в горизонтальную сторону соседней дырки или в край листа. Повторим эту процедуру для всех дырок (рис. слева). После этого лист "распадётся" на некоторое количество m прямоугольников (действительно, у полученных частей все углы прямые).

  У каждого прямоугольника четыре угла, значит, общее число углов всех прямоугольников равно 4m. С другой стороны, к четырём углам исходного листа каждый из 2n разрезов добавляет не более шести прямых углов (см. рис. слева, некоторые углы, образованные каким-то разрезом, могут совпадать с углами, образованными другими разрезами), поэтому число углов не превосходит  12n + 4.

  Таким образом,  4m ≤ 12n + 4,  то есть  m ≤ 3n + 1.

 Пример. Расположимnдырок так, как показано на рис. справа (каждая следующая по высоте больше предыдущей). Как бы мы не разрезали лист, отмеченные на рисунке  3n+ 1  точек попадут на стороны разных прямоугольников, поэтому их не может быть меньше  3n+ 1.

На  3n + 1  часть.