Назад

Олимпиадная задача по планиметрии: площадь четырёхугольника в трапеции

Задача 198468 • Сложность: 2 • 8-9 класс
Задача

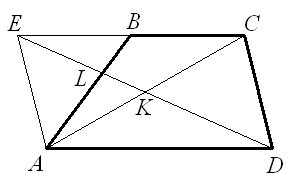
В трапеции ABCD площади 1 основания BC и AD относятся как  1 : 2.&nbsp Пусть K – середина диагонали AC. Прямая DK пересекает сторону AB в точке L. Найдите площадь четырёхугольника BCKL.

Авторы:
Сонкин М.
Разделы:
Планиметрия
Источники:
Турнир городов 21 турнир (1999/2000 год) весенний тур, тренировочный вариант, 8-9 класс Олимпиады и турниры
Количество версий:
5
Решение

  Рассмотрим параллелограмм ADCE. (см. рис.). Тогда K – точка пересечения его диагоналей.  EC = AD = 2BC,  то есть B – середина отрезка EC. AB и EK – медианы треугольника ACE. По известному свойству медиан  AL = ⅔ AB.

 SACD= 2SBAC  (у этих треугольников высоты равны, а основание первого вдвое больше основания второго). Значит,  SBAC= ⅓SABCD= ⅓, SLAK= ⅔·½SBAC=1/9, SBCKL = SBAC – SLAK=2/9.
Ответ

2/9.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет