Олимпиадная задача по алгебраическим неравенствам и индукции для 10-11 классов
Задача
Докажите неравенство 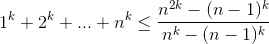 при любых натуральных n и k.
при любых натуральных n и k.
Решение
После умножения обеих частей неравенства на знаменатель правой части и приведения подобных членов получим:
(1k + 2k + … + (n – 1)k)nk ≤ (2k + 3k + ... + nk)(n – 1)k.
Таким образом, достаточно убедиться в справедливости неравенства (m – 1)knk ≤ mk(n – 1)k при m = 2, 3, ... , n. Это просто:
(m – 1)knk ≤ mk(n – 1)k ⇔ (m – 1)n ≤ m(n – 1) ⇔ m ≤ n.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет