Олимпиадная задача по планиметрии о точках X, Y и Z в треугольнике ABC
Задача
В треугольнике ABC точка X лежит на стороне AB, а точка Y – на стороне BC. Отрезки AY и CX пересекаются в точке Z. Известно, что AY = CY и
AB = CZ. Докажите, что точки B, X, Z и Y лежат на одной окружности.
Решение
Решение 1: Продолжим отрезок AY за точку Y на отрезок YD = YB. Треугольники ABY и CDY равны по двум сторонам и углу между ними. Отсюда CD = AB = CZ, то есть треугольник DCZ – равнобедренный. Значит, ∠DZC = ∠D = ∠B, поэтому четырёхугольник BXZY – вписанный.
Решение 2: По теореме синусов из треугольников ABY и YZC получим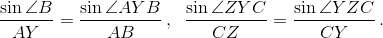 
Так как AB = CZ, AY = CY и
sin ∠AYB = sin ∠ZYC (эти углы в сумме дают 180°), то sin ∠B = sin ∠YZC = sin ∠YZX.
Поскольку углы YZX и B не равны (∠YZX > ∠AXC > ∠B), то ∠YZX + ∠B = 180°, и, значит, четырёхугольник BXZY – вписанный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь