Олимпиадная задача о сумме номеров диагонали на шахматной доске для классов 9–11

  Оценка. Рассмотрим числа  a₁ < a₂ < ... < a₈,  стоящие на чёрной диагонали (конечно, на диагонали они могут стоять не по порядку). Тогда  a₁ ≥ 1,  a₂ ≥ 3,  a₃ ≥ 5,  ...,  a₇ ≥ 13.  Докажем, что  a₈ ≥ 39.

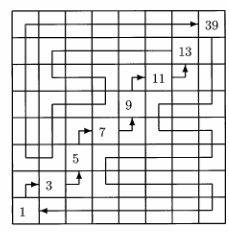
  Предположим, что числа в клетки доски вписывались в порядке их возрастания. Тогда в тот момент, когда на диагональ вписывалось восьмое число, покидаемая половина доски была заполнена (ибо в неё уже не возвращались). Эта половина (включая диагональ) содержит 36 клеток: 16 белых и 20 чёрных. Но при заполнении доски белые и чёрные клетки чередуются. Поэтому к этому моменту были заполнены ещё как минимум три белые клетки в другой половине доски, то есть всего было заполнено не меньше 39 клеток.

  1 + 3 + 5 + ... + 13 + 39 = 88.

  Пример изображён на рисунке.