Олимпиадная задача по планиметрии: угол между прямыми A₃B₃ и A₄B₄, 9–11 класс
Задача
На плоскости даны два отрезка A1B1 и A2B2, причём A2B2/A1B1 = k < 1. На отрезке A1A2 взята точка A3, а на продолжении этого отрезка за точку А2 – точка А4 так, что A3А2/А3А1 = А4А2/А4А1 = k. Аналогично на отрезке В1В2 берётся точка В3, а на продолжении этого отрезка за точку В2 – точка В4 так, что
В3В2/В3В1 = В4В2/В4В1 = k. Найти угол между прямыми А3В3 и А4В4.
Решение
Решение 1: Пусть O – центр не сохраняющего ориентацию подобия, переводящего A1 в A2 и B1 в B2. Так как треугольники OA1B1 и OA2B2 подобны,
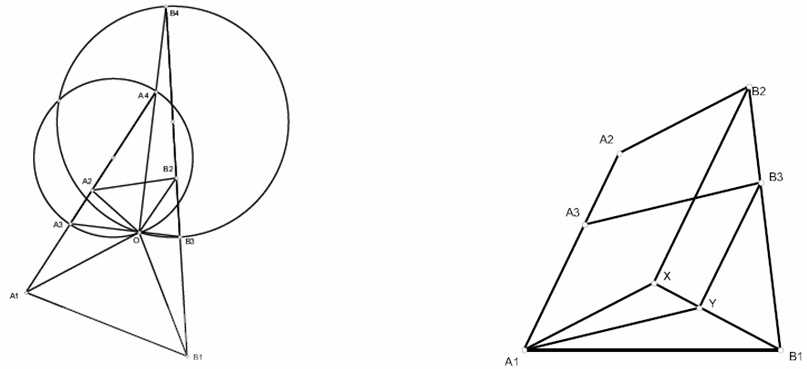
∠A1OB1 = ∠B2OA2 и биссектрисы углов A1OA2 и B1OB2 совпадают. Так как OA2 : OA1 = OB2 : OB1 = k, эта общая биссектриса пересекает отрезки A1A2 и B1B2 в точках A3 и B3, а перпендикулярная ей прямая пересекает продолжения этих отрезков в точках A4 и B4 (рис. слева). Следовательно, искомый угол прямой.
Решение 2: Пусть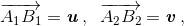 
по условию |v|² = k²|u|². Тогда 
(*)
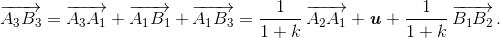С другой стороны,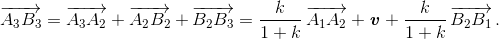 
(**)
Умножив (*) на k/1+k, (**) на 1/1+k и сложив полученные равенства, имеем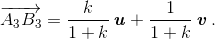 
Аналогично получаем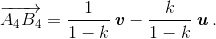 
Отсюда 
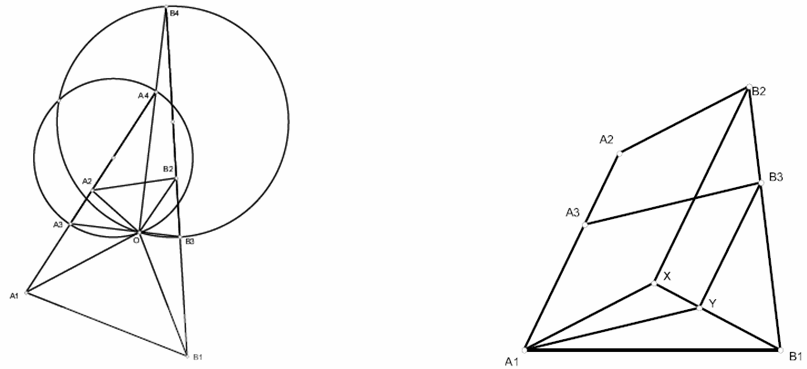то есть векторы ортогональны.
Решение 3:
Построим параллелограмм A1A2B2X и проведём биссектрису A1Y треугольника A1XB1 (рис. справа). Так как B1Y/XY = A1B1/A1X = k, то B3Y || B2X иB3Y = kB2X = A1A3. Следовательно, A1A3B3Y – параллелограмм, то есть A3B3 || A1Y.
Аналогично прямая A4B4 параллельна внешней биссектрисе угла XA1B1, и, значит, прямые A3B3 и A4B4 перпендикулярны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь